Algorithm

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]

示例 2:

输入: nums = [1], k = 1 输出: [1]

说明：你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。

解答：

使用桶排序，倒序获取最高频率k的元素，时间复杂度O(n)，空间复杂度O(n)。

class Solution {
    public List<Integer> topKFrequent(int[] nums, int k) {
        Map<Integer, Integer>  frequentMap = new HashMap<>();
        for (int num: nums ) {
            frequentMap.put(num, frequentMap.getOrDefault(num, 0) + 1);
        }

        List<Integer>[] bucket = new List[nums.length + 1];
        for (int key: frequentMap.keySet()){
            int frequance = frequentMap.get(key);
            if (bucket[frequance] == null){
                bucket[frequance] = new ArrayList<>();
            }

            bucket[frequance].add(key);
        }

        List<Integer> topK = new ArrayList<>();
        for (int pos = bucket.length - 1; pos >= 0 && topK.size() < k; pos--){
            if (bucket[pos] != null){
                topK.addAll(bucket[pos]);
            }
        }

        return topK;
    }   
}

Review

Applying the Linus Torvalds “Good Taste” Coding Requirement

重点谈到了一点：边界情况越少越好，在代码中的实际表现形式就是条件语句的数量越少越好，因此需要测试的分支也会相应减少。

此外，还附带了一些好处，比如：更少的代码行数、复杂度的降低、效率的提升等等。

示例1（源自Linus）：

链表元素删除

Bad：

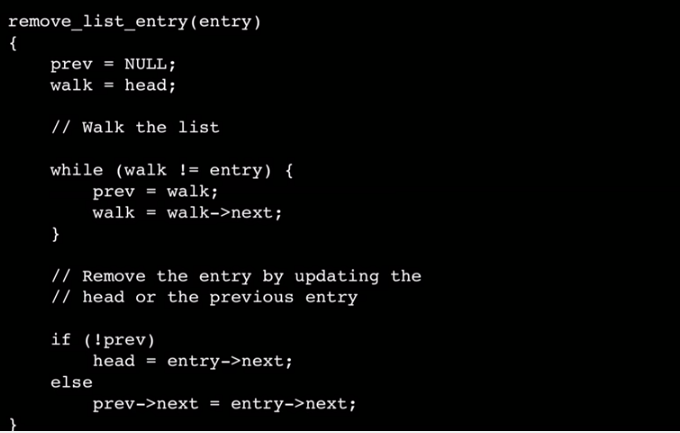
Good：

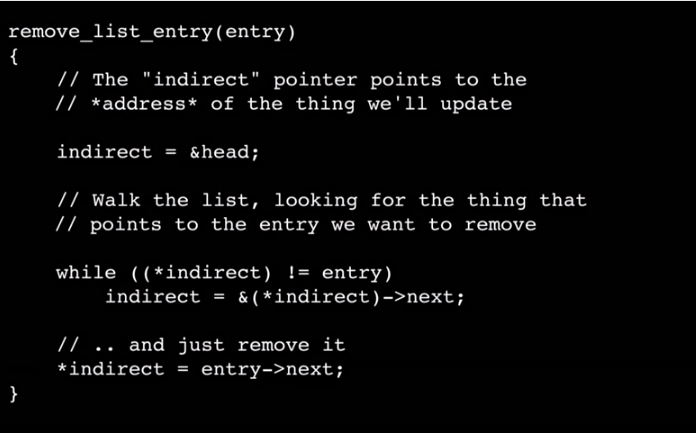
示例2（源自作者）：

网格边缘初始化算法，网格为多维数组：grid[rows][cols]。其目的是初始化网格的边缘，比如：顶行、底行、最左列及最右列。

Bad：

双重for循环，多个条件表达式。

for (r = 0; r < GRID_SIZE; ++r) {
    for (c = 0; c < GRID_SIZE; ++c) {
        // Top Edge
        if (r == 0)
            grid[r][c] = 0;
        // Left Edge
        if (c == 0)
            grid[r][c] = 0;
        // Right Edge
        if (c == GRID_SIZE - 1)
            grid[r][c] = 0;
        // Bottom Edge
        if (r == GRID_SIZE - 1)
            grid[r][c] = 0;
    }
}

Impove：

消除内嵌for循环。

for (i = 0; i < GRID_SIZE * 4; ++i) {
    // Top Edge
    if (i < GRID_SIZE)
        grid[0][i] = 0;
    // Right Edge
    else if (i < GRID_SIZE * 2)
        grid[i - GRID_SIZE][GRID_SIZE - 1] = 0;
    // Left Edge
    else if (i < GRID_SIZE * 3)
        grid[i - (GRID_SIZE * 2)][0] = 0;
    // Bottom Edge
    else
        grid[GRID_SIZE - 1][i - (GRID_SIZE * 3)] = 0;
}

Good：

消除所有的条件语句。

for (i = 0; i < GRID_SIZE; ++i) {
    // Top Edge
    grid[0][i] = 0;
    
    // Bottom Edge
    grid[GRID_SIZE - 1][i] = 0;
    // Left Edge
    grid[i][0] = 0;
    // Right Edge
    grid[i][GRID_SIZE - 1] = 0;
}

两个词来形容：简单&优雅。

上述示例仅仅是小规模代码实现级别的tasty，但这种思路还可应用于大规模的软件设计上，对Good Taste开发者总结如下：

在实现之前要把时间花在概念化将要构造的内容上，来定义使用到的组件的边界和它们之间的相互协作，确保它们能够优雅地融合和执行。

Tip

写Algorithm算法题用到的Idea快捷键，通过这些快捷键基本上就不需要使用鼠标操作了，因此总结下无鼠标操作快捷键的最小集：

在Idea上创建类没有快捷键，但可以使用Command+N间接完成。
Command+1：切换工作区
Control+Tab：打开文件切换
Command+E：切换文件
Ctrl+Shift+r：执行测试用例
Command+B：跳转到定义
Command+[：回到上次操作位置
Command+4：查看测试用例执行
Shift+F6：重命名
Control+左箭头/右箭头：mac系统窗口切换

一些常规快捷键未列出，比如：Command+S等，另外文本编辑使用了大量vi来完成。

其他可选快捷键：

Command+O：类查询
Command+Shift：文件查询
Control+W：横向分屏

关于CAP理论有两个版本定义：

第一版

Any distributed system cannot guaranty C, A, and P simultaneously.

第二版

In a distributed system (a collection of interconnected nodes that share data.), you can only have two out of the following three guarantees across a write/read pair: Consistency, Availability, and Partition Tolerance - one of them must be sacrificed.

第一版更加通俗易懂，流传比较广泛，第二版则更加精准。

第二版增加了一些分布式系统的限定：

interconnected 和 share data。分布式系统并不一定会互联和共享数据，比如：Memcache集群。
write/read pair。CAP关注数据的读写操作，而非其他功能。比如：ZooKeeper 的选举机制。

References

https://medium.com/@bartobri/applying-the-linus-tarvolds-good-taste-coding-requirement-99749f37684a
http://robertgreiner.com/2014/06/cap-theorem-explained/
http://www.infoq.com/cn/articles/cap-twelve-years-later-how-the-rules-have-changed

版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 3.0 许可协议。转载请注明出处！

ARTS01

Algorithms-Review- Tip-Share

Algorithm

Review

Tip

References

CATALOG

FEATURED TAGS

FRIENDS