
蒙特卡洛方法介绍
前言
不久前参加了邓辉、孙鸣老师的《机器学习之旅》的培训。在培训课堂上邓辉老师对AlphaGO的架构以及实现进行了介绍,其中涉及AlphaGO的的多项关键技术,其中之一就是蒙特卡洛方法(除外还包括快速走子、走棋网络以及估值网络)。当时听得一知半解,仅仅知其然但不知其所以然。经过一段时间的学习研究,想通过这篇文章来做一个过程性总结。
围棋的不同
早在1996年,深蓝就战胜了国际象棋大师卡斯帕罗夫,成为首个在标准比赛时限内击败国际象棋世界冠军的电脑系统。随着计算机能力的不断增强,计算机的计算、存储能力都是人类望尘莫及的,在人们脑海中计算机战胜人类不是理所应当的吗?直到今年Google DeepMind挑战李世石成功引起的轰动效应,才发现事情没那么简单。 那么为什么围棋这一难题在深蓝胜利之后的20年才被计算机攻克呢?围棋与其他棋类差别究竟在哪呢?对于这些问题还是需要回归到棋力的要求说起,评价一个优秀棋手的能力无非是从计算能力和对棋局的评判能力说起,下面将分别说明:
计算能力要求的不同
首先,国际象棋的棋盘大小为64(88),围棋的大小为361(1919)。由于棋盘大小的不同,每走一步国际象棋和围棋的计算量的要求是不一样的,围棋明显要求更高。这在博弈论中一般称之为分支因子,即平均每个落子后的合法走法,国际象棋的分支因子约为35,而围棋大约是250。另外一个可以说明计算能力要求不同的指标是搜索空间,在该指标上两者也存在指数级的差异,国际象棋是10^50,而围棋是10^171。我们知道宇宙中的原子总数总共大约也才10^80,因此围棋的搜索空间绝对算是天文数字。
棋局评判能力要求的不同
棋局的评判一般使用估值函数来评估,国际象棋的棋局局面特征比较明显,最容易想到的是可以给每个棋子设置不同的分值,对弈双方算下各自总分来看哪一方更占据优势。如果再加上一定的位置特征(比如棋子在不同的位置有不同的加减分),棋子的行动力,棋子之间的保护关系等特征,对局面的评价就已经很靠谱了。而对于围棋上述方法基本不起任何作用,差一个棋子的盘面都可能是翻天覆地的。但既然高手能在几百个选择中知道哪几个位置值得考虑,说明它的估值函数还是存在有且规律可循的。
蒙特卡洛方法
最终人们通过蒙特卡洛方法来解决这一难题。那么什么是蒙特卡洛方法呢?蒙特卡罗方法又称统计模拟法、随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。 通俗地讲蒙特卡洛方法是在一箱苹果中挑选一个最红苹果,每次都从箱子中随机拿出一个苹果,然后和手中的苹果比较,如果拿出的苹果比较红则用该苹果替换手中的苹果,如果手中的比较红则不进行替换。这样手中的苹果会越来越红。如果重复次数足够多的话则一定会找到那个最红的苹果。 蒙特卡洛方法一般用于三类不同的问题:优化、数值积分及根据概率分布生成图形。最典型的例子是计算圆周率π,计算步骤如下:
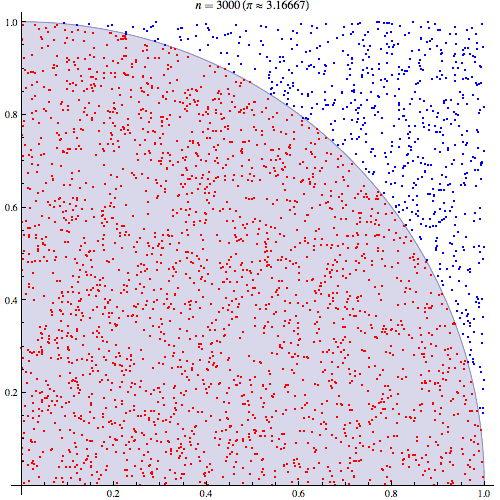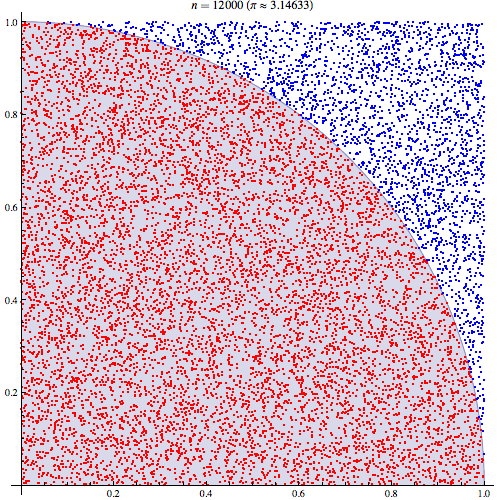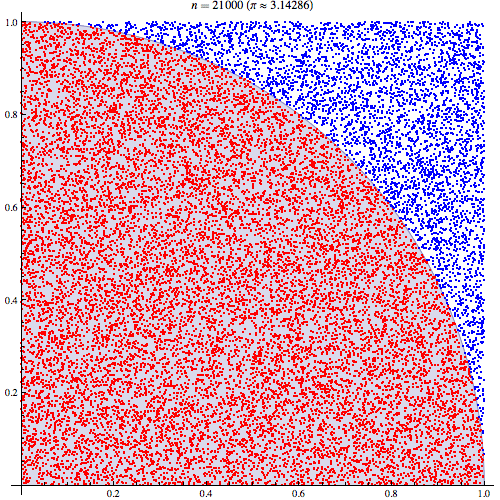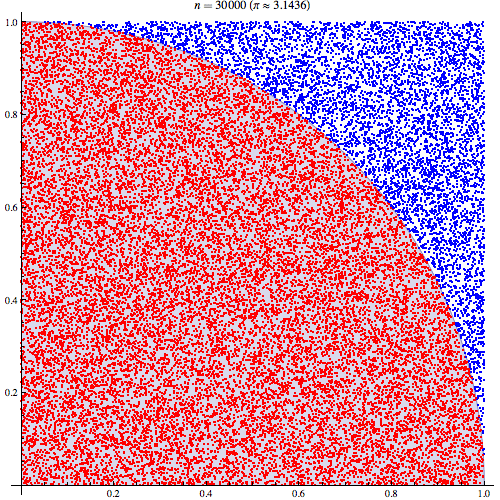
-
首先以中心为原点绘制一个正方形,并在其内画一个圆形。
-
在坐标(x>0, y>0)的正方形区域内随机打点。
-
数出在圆内总共的点数。
4.将圆内点数除以总共的打点数,然后再乘以4就可以得到圆周率π的近似值。
python实现示例:
import random
import math
import sys
def calc_pi(num):
valid_points = filter(lambda (x, y): math.sqrt(x*x + y*y) < 1, _generator_point_list(num))
return (len(valid_points)) * 4/ float(num)
def _generator_point_list(num):
return [(random.random(), random.random()) for _ in range(num) ]
小试牛刀一下,是不是很酷?
- 版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 许可协议。转载请注明出处!
